Introduction

The One Sample t-test is a fundamental statistical tool used in research to test whether the mean of a sample is significantly different from a known or hypothesized population mean. It is widely used in social sciences, business research, healthcare, and education to validate assumptions and support decision-making.

What is a One Sample t-Test?

The One Sample t-test checks whether the average value of a sample differs significantly from a specified population mean, when the population standard deviation is unknown.

When should we use it?

Use a One Sample t-test when:

• You have one sample group.
• You want to test whether the sample mean is significantly different from a known/or hypothesized population mean (Assumed/benchmark mean).
• Your dependent variable is continuous (e.g., height, weight, scores).
• The population standard deviation is unknown.
• Your sample is normally distributed (or approximately normal if n > 30).

Note: The hypothesized population mean is the value we assume to be true about the population before conducting a statistical test (like the one-sample t-test or z-test). It represents the benchmark or expected average that our sample is being compared against.  The assumption may be based on past data/historical data or past experience, etc.

In Technical Terms:

It is the value of the population mean (μ) that is assumed under the null hypothesis (H₀).

So, when you run a one-sample t-test, you’re testing:

H₀: μ = μ₀,
where μ₀ is the hypothesized population mean.

One Sample ‘t’ test Formula

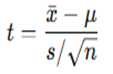
Where

x̄  = Sample Mean

μ = Population Mean

s = Sample Standard deviation (SD)

n = Sample Size

Hypothesis Structure

Null Hypothesis (H₀): The sample mean is equal to the population mean

Alternative Hypothesis (H₁): The sample mean is different from the population mean (two-tailed) or greater/less (one-tailed)

(OR)

Null Hypothesis (H₀): There is no difference between sample mean and population mean.

H₀: μ = μ₀

Alternative Hypothesis (H₁): There is a significant different between sample mean and population mean.

H₀: μ ≠ μ₀ (Two-tailed test)

H₀: μ > μ₀ (One-tailed test, right-tailed)

H₀: μ < μ₀ (One-tailed test, left-tailed)

Practical Examples from different Domains

1. HR Domain – Employee Satisfaction

Scenario: A company claims its average employee satisfaction score is 4.0 (on a 5-point scale). A researcher collects responses from 30 employees and finds the sample mean = 3.7, SD = 0.5.

Objective: Is employee satisfaction significantly lower than claimed?

• H₀: µ = 4.0
• H₁: µ < 4.0 (one-tail test/left-tailed test)
• Use t-test to check if the gap is statistically significant.

2. Marketing – Customer Perception

Scenario: A brand claims its latest product has an average perceived quality rating of 8/10. A sample of 50 consumers reports a mean of 7.6, SD = 1.1.

Objective: Validate the claim using a One Sample t-test.

• H₀: µ = 8 (Two-tailed test)
• H₁: µ ≠ 8
• A significant t-value (p < 0.05) may lead to questioning the brand’s claim.

3. Education – Exam Scores

Scenario: The national average score for a standardized test is 70. A teacher wants to know if their class of 25 students is performing better. The class average is 73, SD = 5.

• H₀: µ = 70
• H₁: µ > 70 (one-tailed test/right-tailed test)
• A positive, significant t-value indicates better performance.

4. Psychology – Anxiety Levels

Scenario: A psychologist wants to test whether a stress-reduction program lowers anxiety below the normative mean of 50. After the program, the anxiety scores of 12 participants average 46, SD = 3.5.

• H₀: µ = 50
• H₁: µ < 50
• If p < 0.05, the program is effective.

5. Tourism – Guest Satisfaction

Scenario: A resort claims average guest satisfaction of 4.5 stars. A tourism researcher collects feedback from 20 guests, finding a mean of 4.2, SD = 0.4.

• H₀: µ = 4.5
• H₁: µ ≠ 4.5
• Use the t-test to assess if guests are actually less satisfied than claimed.

How to run a One Sample t-Test in SPSS

1. Open SPSS and enter your data.
2. Go to Analyze → Compare Means → One-Sample T Test.
3. Select the test variable (e.g., Satisfaction).
4. Enter the test value (e.g., 4.5).
5. Click OK.

SPSS Output Includes:

• Sample Mean
• t-value
• Degrees of Freedom
• p-value

Interpretation: If p < 0.05, reject the null hypothesis (Reject H₀: There is no difference)

Visual Tip: Interpret Results in simple language

• If p < 0.05 → “There is a statistically significant difference between the sample mean and the population mean.”
• If p ≥ 0.05 → “There is no statistically significant difference.”

Summary Table: One Sample t-Test use Cases

Domain	Hypothesis*	Use Cases
HR	µ = 4.0	Is employee satisfaction lower than expected?
Marketing	µ = 8.0	Does customer rating align with product promise?
Education	µ = 70	Are students performing above national average?
Psychology	µ = 50	Is therapy reducing anxiety below the standard threshold?
Tourism	µ = 4.5	Are guests actually satisfied at claimed levels?

Note: Hypothesis* – Population Mean or Hypothesized Population Mean

Conclusion

The One Sample t-test is a flexible and widely applicable tool. It allows researchers and practitioners across industries to validate claims, assess performance, and support data-driven decisions. Use it wisely when you have one group, have a known benchmark and want to test how close reality is to expectation.

Contact us if you need any assistance!